Fermat number
In mathematics, a Fermat number, named after Pierre de Fermat who first studied them, is a positive integer of the form
where n is a nonnegative integer. The first few Fermat numbers are:
- 3, 5, 17, 257, 65537, 4294967297, 18446744073709551617, … (sequence A000215 in OEIS).
If 2n + 1 is prime, and n > 0, it can be shown that n must be a power of two. (If n = ab where 1 ≤ a, b ≤ n and b is odd, then 2n + 1 = (2a)b + 1 ≡ (−1)b + 1 = 0 (mod 2a + 1). See below for complete proof.) In other words, every prime of the form 2n + 1 is a Fermat number, and such primes are called Fermat primes. The only known Fermat primes are F0, F1, F2, F3, and F4.
Basic properties
The Fermat numbers satisfy the following recurrence relations:
for n ≥ 1,
for n ≥ 2. Each of these relations can be proved by mathematical induction. From the last equation, we can deduce Goldbach's theorem: no two Fermat numbers share a common factor. To see this, suppose that 0 ≤ i < j and Fi and Fj have a common factor a > 1. Then a divides both
and Fj; hence a divides their difference, 2. Since a > 1, this forces a = 2. This is a contradiction, because each Fermat number is clearly odd. As a corollary, we obtain another proof of the infinitude of the prime numbers: for each Fn, choose a prime factor pn; then the sequence {pn} is an infinite sequence of distinct primes.
Further properties:
- The number of digits D(n,b) of Fn expressed in the base b is
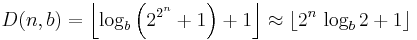 (See floor function).
(See floor function).
- No Fermat number can be expressed as the sum of two primes, with the exception of F1 = 2 + 3.
- No Fermat prime can be expressed as the difference of two pth powers, where p is an odd prime.
- With the exception of F0 and F1, the last digit of a Fermat number is 7.
- The sum of the reciprocals of all the Fermat numbers (sequence A051158 in OEIS) is irrational. (Solomon W. Golomb, 1963)
Primality of Fermat numbers
Fermat numbers and Fermat primes were first studied by Pierre de Fermat, who conjectured (but admitted he could not prove) that all Fermat numbers are prime. Indeed, the first five Fermat numbers F0,...,F4 are easily shown to be prime. However, this conjecture was refuted by Leonhard Euler in 1732 when he showed that
Euler proved that every factor of Fn must have the form k2n+2 + 1.
The fact that 641 is a factor of F5 can be easily deduced from the equalities 641 = 27×5+1 and 641 = 24 + 54. It follows from the first equality that 27×5 ≡ −1 (mod 641) and therefore (raising to the fourth power) that 228×54 ≡ 1 (mod 641). On the other hand, the second equality implies that 54 ≡ −24 (mod 641). These congruences imply that −232 ≡ 1 (mod 641).
It is widely believed that Fermat was aware of the form of the factors later proved by Euler, so it seems curious why he failed to follow through on the straightforward calculation to find the factor.[1] One common explanation is that Fermat made a computational mistake and was so convinced of the correctness of his claim that he failed to double-check his work.
There are no other known Fermat primes Fn with n > 4. However, little is known about Fermat numbers with large n.[2] In fact, each of the following is an open problem:
- Is Fn composite for all n > 4?
- Are there infinitely many Fermat primes? (Eisenstein 1844)[3]
- Are there infinitely many composite Fermat numbers?
As of 2010[update] it is known that Fn is composite for 5 ≤ n ≤ 32, although complete factorizations of Fn are known only for 0 ≤ n ≤ 11, and there are no known factors for n in {20, 24}.[4] The largest Fermat number known to be composite is F2543548, and its prime factor 9×22543551 + 1 was discovered by Scott Brown in PrimeGrid's Proth Prime Search on June 22, 2011.
Heuristic arguments for density
The following heuristic argument suggests there are only finitely many Fermat primes: according to the prime number theorem, the "probability" that a number n is prime is at most A/ln(n), where A is a fixed constant. Therefore, the total expected number of Fermat primes is at most
It should be stressed that this argument is in no way a rigorous proof. For one thing, the argument assumes that Fermat numbers behave "randomly", yet we have already seen that the factors of Fermat numbers have special properties. If (more sophisticatedly) we regard the conditional probability that n is prime, given that we know all its prime factors exceed B, as at most Aln(B)/ln(n), then using Euler's theorem that the least prime factor of Fn exceeds 2n + 1, we would find instead
Although such arguments engender the belief that there are only finitely many Fermat primes, one can also produce arguments for the opposite conclusion. Suppose we regard the conditional probability that n is prime, given that we know all its prime factors are 1 modulo M, as at least CM/ln(n). Then using Euler's result that M = 2n + 1 we would find that the expected total number of Fermat primes was at least
and indeed this argument predicts that an asymptotically constant fraction of Fermat numbers are prime!
Equivalent conditions of primality
There are a number of conditions that are equivalent to the primality of Fn.
- Proth's theorem (1878) — Let N = k2m + 1 with odd k < 2m. If there is an integer a such that
- then N is prime. Conversely, if the above congruence does not hold, and in addition
-
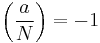 (See Jacobi symbol)
(See Jacobi symbol)
- then N is composite. If N = Fn > 3, then the above Jacobi symbol is always equal to −1 for a = 3, and this special case of Proth's theorem is known as Pépin's test. Although Pépin's test and Proth's theorem have been implemented on computers to prove the compositeness of many Fermat numbers, neither test gives a specific nontrivial factor. In fact, no specific prime factors are known for n = 20 and 24.
- Let n ≥ 3 be a positive odd integer. Then n is a Fermat prime if and only if for every a co-prime to n, a is a primitive root mod n if and only if a is a quadratic nonresidue mod n.
- The Fermat number Fn > 3 is prime if and only if it can be written uniquely as a sum of two nonzero squares, namely
- When
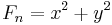 not of the form shown above, a proper factor is:
not of the form shown above, a proper factor is:
- Example 1: F5 = 622642 + 204492, so a proper factor is
- Example 2: F6 = 40468032562 + 14387937592, so a proper factor is
Factorization of Fermat numbers
Because of the size of Fermat numbers, it is difficult to factorize or to prove primality of those. Pépin's test gives a necessary and sufficient condition for primality of Fermat numbers, and can be implemented by modern computers. The elliptic curve method is a fast method for finding small prime divisors of numbers. Distributed computing project Fermatsearch has successfully found some factors of Fermat numbers. Yves Gallot's proth.exe has been used to find factors of large Fermat numbers. Édouard Lucas, improving the above mentioned result by Euler, proved in 1878 that every factor of Fermat number 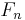 , with n at least 2, is of the form
, with n at least 2, is of the form 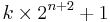 (see Proth number), where k is a positive integer; this is in itself almost sufficient to prove the primality of the known Fermat primes.
(see Proth number), where k is a positive integer; this is in itself almost sufficient to prove the primality of the known Fermat primes.
Factorizations of the first ten Fermat numbers are:
| F0 | = | 21 | + | 1 | = | 3 is prime | |
| F1 | = | 22 | + | 1 | = | 5 is prime | |
| F2 | = | 24 | + | 1 | = | 17 is prime | |
| F3 | = | 28 | + | 1 | = | 257 is prime | |
| F4 | = | 216 | + | 1 | = | 65,537 is the largest known Fermat prime | |
| F5 | = | 232 | + | 1 | = | 4,294,967,297 | |
| = | 641 × 6,700,417 | ||||||
| F6 | = | 264 | + | 1 | = | 18,446,744,073,709,551,617 | |
| = | 274,177 × 67,280,421,310,721 | ||||||
| F7 | = | 2128 | + | 1 | = | 340,282,366,920,938,463,463,374,607,431,768,211,457 | |
| = | 59,649,589,127,497,217 × 5,704,689,200,685,129,054,721 | ||||||
| F8 | = | 2256 | + | 1 | = | 115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,913,129,639,937 | |
| = | 1,238,926,361,552,897 × 93,461,639,715,357,977,769,163,558,199,606,896,584,051,237,541,638,188,580,280,321 | ||||||
| F9 | = | 2512 | + | 1 | = | 13,407,807,929,942,597,099,574,024,998,205,846,127,479,365,820,592,393,377,723,561,443,721,764,030,073,546,976,801,874,298,166,903,427,690,031,858,186,486,050,853,753,882,811,946,569,946,433,649,006,084,097 | |
| = | 2,424,833 × 7,455,602,825,647,884,208,337,395,736,200,454,918,783,366,342,657 × 741,640,062,627,530,801,524,787,141,901,937,474,059,940,781,097,519,023,905,821,316,144,415,759,504,705,008,092,818,711,693,940,737 | ||||||
| F10 | = | 21024 | + | 1 | = | 179769313 4862315907 7293051907 8902473361 7976978942 3065727343 0081157732 6758055009 6313270847 7322407536 0211201138 7987139335 7658789768 8144166224 9284743063 9474124377 7678934248 6548527630 2219601246 0941194530 8295208500 5768838150 6823424628 8147391311 0540827237 1633505106 8458629823 9947245938 4797163048 3535632962 4224137217 | |
| = | 45592577 × 6487031809 × 4659775785 2200185432 6456074307 6778192897 ×
13 0439874405 4881897274 8476879650 9903946608 5308416118 9218689529 5776832416 2514718635 7414022797 7573104895 8987839288 4292384483 1149032913 7987290886 0161794609 4119449010 5959067101 3053190617 1018354491 6096191939 1248853811 6080712299 6723228062 1782075312 7014424577 |
||||||
| F11 | = | 22048 | + | 1 | = | 3231700 6071311007 3007148766 8866995196 0444102669 7154840321 3034542752 4655138867 8908931972 0141152291 3463688717 9609218980 1949411955 9150490921 0950881523 8644828312 0630877367 3009960917 5019775038 9652106796 0576383840 6756827679 2218642619 7561618380 9433847617 0470581645 8520363050 4288757589 1541065808 6075523991 2393038552 1914333389 6683424206 8497478656 4569494856 1760353263 2205807780 5659331026 1927084603 1415025859 2864177116 7259436037 1846185735 7598351152 3016459044 0369761323 3287231227 1256847108 2020972515 7101726931 3234696785 4258065669 7935045997 2683529986 3821552516 6389437335 5436021354 3322960464 5318478604 9521481935 5585361105 9596230657 | |
| = | 319489 × 974849 × 1 6798855634 1760475137 × 35 6084190644 5833920513 ×
1734 6244717914 7555430258 9708643097 7837742184 4723664084 6493470190 6136357919 2879108857 5910383304 0883717798 3810868451 5464219407 1297830613 4189864280 8260145427 5870858924 3873685563 9731189488 6939915854 5506611147 4202161325 5701726056 4139394366 9457932209 6866510895 9685482705 3880726458 2855415193 6401912464 9311825460 9287981573 3057795573 3585049822 7928009094 2872567591 5189121186 2275171431 9229788100 9792510360 3549691727 9912663527 3587832366 4719315477 7091427745 3770382945 8491891759 0325110939 3813224860 4429857397 1650711059 2444621775 4254070691 3047034664 6436034913 8244172330 6598834177 |
As of January 2011[update], only F0 to F11 have been completely factored.[4] The distributed computing project Fermat Search is searching for new factors of Fermat numbers.[5] The set of all Fermat factors is A050922 (or, sorted, A023394) in OEIS.
Pseudoprimes and Fermat numbers
Like composite numbers of the form 2p − 1, every composite Fermat number is a strong pseudoprime to base 2. Because all strong pseudoprimes to base 2 are also Fermat pseudoprimes - i.e.
for all Fermat numbers.
Because it is generally believed that all but the first few Fermat numbers are composite, this makes it possible to generate infinitely many strong pseudoprimes to base 2 from the Fermat numbers.
In fact, Rotkiewicz showed in 1964 that the product of any number of prime or composite Fermat numbers will be a Fermat pseudoprime to base 2.
Other theorems about Fermat numbers
Lemma: If n is a positive integer,
proof:
Theorem: If 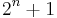 is an odd prime, then
is an odd prime, then  is a power of 2.
is a power of 2.
proof:
If  is a positive integer but not a power of 2, then
is a positive integer but not a power of 2, then 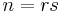 where
where 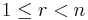 ,
, 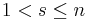 and
and  is odd.
is odd.
By the preceding lemma, for positive integer  ,
,
where  means "evenly divides". Substituting
means "evenly divides". Substituting 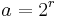 ,
, 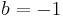 , and
, and 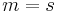 and using that
and using that  is odd,
is odd,
and thus
Because 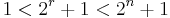 , it follows that
, it follows that 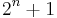 is not prime. Therefore, by contraposition
is not prime. Therefore, by contraposition  must be a power of 2.
must be a power of 2.
Theorem: A Fermat prime cannot be a Wieferich prime.
Proof: We show if 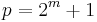 is a Fermat prime, then the congruence
is a Fermat prime, then the congruence 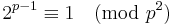 does not satisfy.
does not satisfy.
It is easy to show 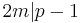 . Now write,
. Now write, 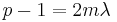 . If the given congruence satisfies, then
. If the given congruence satisfies, then 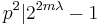 , therefore
, therefore
Hence 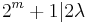 ,and therefore
,and therefore 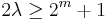 . This leads to
. This leads to
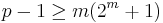 , which is impossible since
, which is impossible since 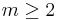 .
.
A theorem of Édouard Lucas: Any prime divisor p of Fn = 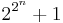 is of the form
is of the form 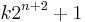 whenever n is greater than one.
whenever n is greater than one.
Sketch of proof:
Let Gp denote the group of non-zero elements of the integers (mod p) under multiplication, which has order p-1. Notice that 2 (strictly speaking, its image (mod p)) has multiplicative order 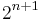 in Gp, so that, by Lagrange's theorem, p-1 is divisible by
in Gp, so that, by Lagrange's theorem, p-1 is divisible by 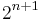 and p has the form
and p has the form 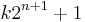 for some integer k, as Euler knew. Édouard Lucas went further. Since n is greater than 1, the prime p above is congruent to 1 (mod 8). Hence (as was known to Carl Friedrich Gauss), 2 is a quadratic residue (mod p), that is, there is integer a such that a2 -2 is divisible by p. Then the image of a has order
for some integer k, as Euler knew. Édouard Lucas went further. Since n is greater than 1, the prime p above is congruent to 1 (mod 8). Hence (as was known to Carl Friedrich Gauss), 2 is a quadratic residue (mod p), that is, there is integer a such that a2 -2 is divisible by p. Then the image of a has order 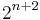 in the group Gp and (using Lagrange's theorem again), p-1 is divisible by
in the group Gp and (using Lagrange's theorem again), p-1 is divisible by 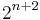 and p has the form
and p has the form 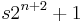 for some integer s.
for some integer s.
In fact, it can be seen directly that 2 is a quadratic residue (mod p), since 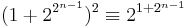 (mod p). Since an odd power of 2 is a quadratic residue (mod p), so is 2 itself.
(mod p). Since an odd power of 2 is a quadratic residue (mod p), so is 2 itself.
Relationship to constructible polygons
An n-sided regular polygon can be constructed with compass and straightedge if and only if n is the product of a power of 2 and distinct Fermat primes. In other words, if and only if n is of the form n = 2kp1p2…ps, where k is a nonnegative integer and the pi are distinct Fermat primes.
A positive integer n is of the above form if and only if its totient φ(n) is a power of 2.
Applications of Fermat numbers
Pseudorandom Number Generation
Fermat primes are particularly useful in generating pseudo-random sequences of numbers in the range 1 … N, where N is a power of 2. The most common method used is to take any seed value between 1 and P − 1, where P is a Fermat prime. Now multiply this by a number A, which is greater than the square root of P and is a primitive root modulo P (i.e., it is not a quadratic residue). Then take the result modulo P. The result is the new value for the RNG.
This is useful in computer science since most data structures have members with 2X possible values. For example, a byte has 256 (28) possible values (0–255). Therefore to fill a byte or bytes with random values a random number generator which produces values 1–256 can be used, the byte taking the output value − 1. Very large Fermat primes are of particular interest in data encryption for this reason. This method produces only pseudorandom values as, after P − 1 repetitions, the sequence repeats. A poorly chosen multiplier can result in the sequence repeating sooner than P − 1.
Other interesting facts
A Fermat number cannot be a perfect number or part of a pair of amicable numbers.(Luca 2000)
The series of reciprocals of all prime divisors of Fermat numbers is convergent.(Krizek, Luca, Somer 2002)
If nn + 1 is prime, there exists an integer m such that n = 22m. The equation nn + 1 = F(2m+m) holds at that time.[6]
Let the largest prime factor of Fermat number Fn be P(Fn). Then,
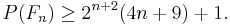 (Grytczuk, Luca and Wojtowicz, 2001)
(Grytczuk, Luca and Wojtowicz, 2001)
Generalized Fermat numbers
Numbers of the form 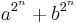 , where a > 1 are called generalized Fermat numbers. By analogy with the ordinary Fermat numbers, it is common to write generalized Fermat numbers of the form
, where a > 1 are called generalized Fermat numbers. By analogy with the ordinary Fermat numbers, it is common to write generalized Fermat numbers of the form 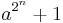 as Fn(a). In this notation, for instance, the number 100,000,001 would be written as F3(10).
as Fn(a). In this notation, for instance, the number 100,000,001 would be written as F3(10).
An odd prime p is a generalized Fermat number if and only if p is congruent to 1 (mod 4) (with the exception of 3 = 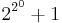 ).
).
Generalized Fermat primes
Because of the ease of proving their primality, generalized Fermat primes have become in recent years a hot topic for research within the field of number theory. Many of the largest known primes today are generalized Fermat primes.
Generalized Fermat numbers can be prime only for even a, because if a is odd then every generalized Fermat number will be divisible by 2. By analogy with the heuristic argument for the finite number of primes among the base-2 Fermat numbers, it is to be expected that there will be only finitely many generalized Fermat primes for each even base. The smallest prime number Fn(a) with n > 4 is F5(30), or 3032+1.
A more elaborate theory can be used to predict the number of bases for which Fn(a) will be prime for a fixed n. The number of generalized Fermat primes can be roughly expected to halve as n is increased by 1.
See also
- Mersenne prime
- Pierpont prime
- Lucas' theorem
- Proth's theorem
- Pseudoprime
- Primality test
- Constructible polygon: which regular polygons are constructible partially depends on Fermat primes.
- Sierpiński number
- Sylvester's sequence
- Double exponential function
Notes
- ^ Křížek, Luca, Somer 2001, p. 38, Remark 4.15
- ^ Chris Caldwell, "Prime Links++: special forms" at The Prime Pages.
- ^ Ribenboim, Paulo (1996), The New Book of Prime Number Records, New York: Springer, p. 88, ISBN 0387944575.
- ^ a b Keller, Wilfrid (January 12, 2011), "Prime Factors of Fermat Numbers", ProthSearch.net, http://www.prothsearch.net/fermat.html#Summary
- ^ FermatSearch.org
- ^ Jeppe Stig Nielsen, "S(n) = n^n + 1".
References
- Golomb, S. W. (1963), "On the sum of the reciprocals of the Fermat numbers and related irrationalities", Canad. J. Math. 15: 475–478
- Grytczuk, A.; Luca, F. & Wojtowicz, M. (2001), "Another note on the greatest prime factors of Fermat numbers", Southeast Asian Bulletin of Mathematics 25 (1): 111–115, doi:10.1007/s10012-001-0111-4
- Guy, Richard K. (2004), Unsolved Problems in Number Theory (3rd ed.), New York: Springer Verlag, pp. A3, A12, B21, ISBN 0387208607
- Křížek, Michal; Luca, Florian & Somer, Lawrence (2001), 17 Lectures on Fermat Numbers: From Number Theory to Geometry, CMS books in mathematics, 10, New York: Springer, ISBN 0387953329 (This book contains an extensive list of references.)
- Křížek, Michal; Luca, Florian & Somer, Lawrence (2002), "On the convergence of series of reciprocals of primes related to the Fermat numbers", Journal of Number Theory 97 (1): 95–112, doi:10.1006/jnth.2002.2782
- Luca, Florian (2000), "The anti-social Fermat number", American Mathematical Monthly 107 (2): 171–173, doi:10.2307/2589441
- Robinson, Raphael M. (1954), "Mersenne and Fermat Numbers", Proceedings of the American Mathematical Society 5 (5): 842–846, doi:10.2307/2031878.
- Yabuta, M. (2001), "A simple proof of Carmichael's theorem on primitive divisors", Fibonacci Quarterly 39: 439–443, http://www.fq.math.ca/Scanned/39-5/yabuta.pdf.
External links
- Chris Caldwell, The Prime Glossary: Fermat number at The Prime Pages.
- Luigi Morelli, History of Fermat Numbers
- John Cosgrave, Unification of Mersenne and Fermat Numbers
- Wilfrid Keller, Prime Factors of Fermat Numbers
- Weisstein, Eric W., "Fermat Number" from MathWorld.
- Yves Gallot, Generalized Fermat Prime Search
- Mark S. Manasse, Complete factorization of the ninth Fermat number (original announcement)
|
|||||||||||||||||||||||||||||
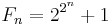
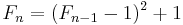
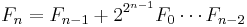
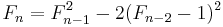

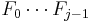
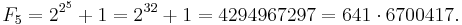
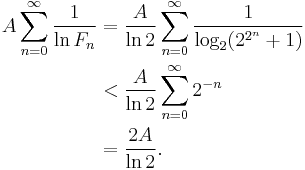
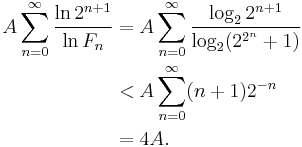
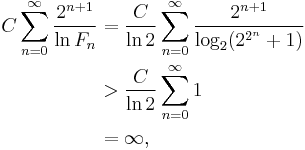
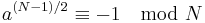
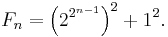
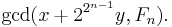
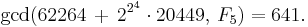
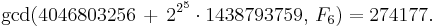

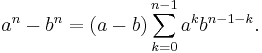
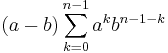
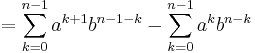
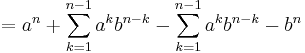
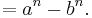
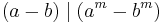
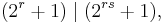
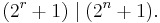
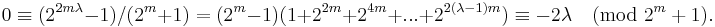
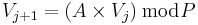 (see
(see